Physical models of wireless channels

Please submit your solutions in Laulima.

A reflecting wall at the transmitter

We have worked on examples where there is a perfectly reflective wall at the receiver. Now let us assume that the wall is at the transmitter.

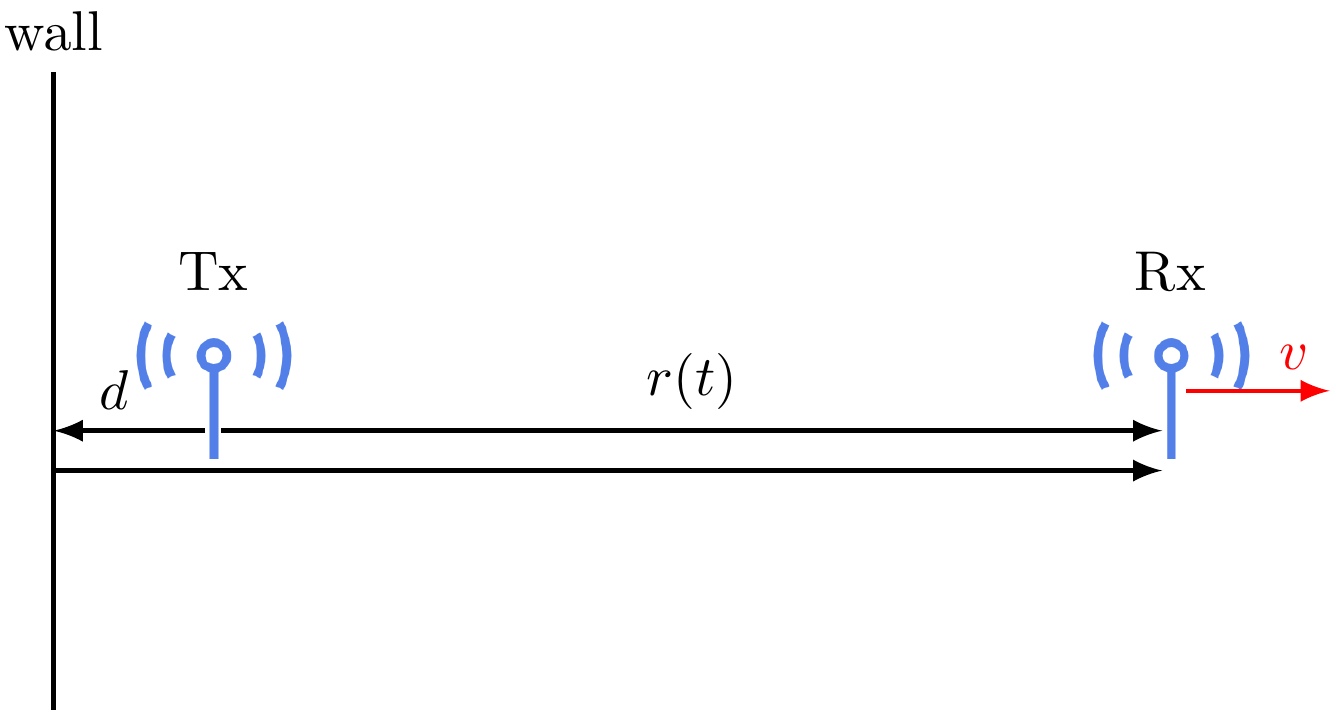
• (1 point) Derive the analytical expression of the received signal using the ray tracing method.
• (2 points) Following the procedure here, derive the coherence distance, the delay spread, and the coherence bandwidth. Compare them with the example when the wall is at the receiver.
• (2 points) Following the procedure here, derive the Doppler spread and the coherence time. Compare them with the example when the wall is at the receiver.

Reflecting on the ground plane

Consider the scenario where the transmit and receive antennas are at different heights. There is a line-of-sight path and a path where the signal is reflected on the ground.

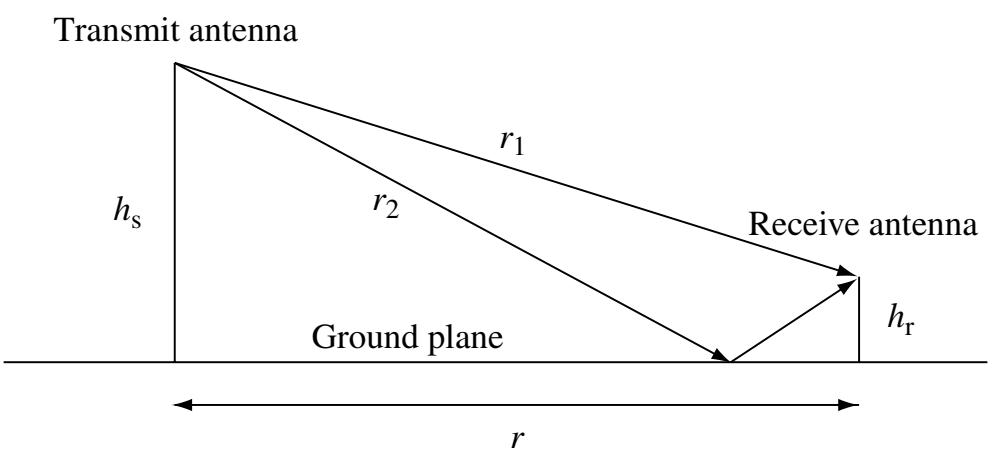
• (1 point) Derive the analytical expression of the received signal using the ray tracing method.
  • We can assume that the ground is a perfect reflector: it does not absorb energy and shifts the phase by \(180^\circ\).
  • Please use the heights \(h_s, h_r\) and the horizontal distance \(r\) as the parameters in the expression.
  • You would need to use some geometry to write \(r_1\) and \(r_2\) as a function of \(h_s, h_r, r\).
• (2 points) Write a Python script to draw the energy of the received signal as a function of the horizontal distance \(r\) between the transmitter and the receiver. Verify that the power scaling law is roughly \(r^{-4}\).
  • You can reuse our code in the experiential learning.
  • You can set the heights of the transmitter and the receiver as \(h_s=30\)m and \(h_r=1\)m, respectively.
  • Note that we derived the signal. For its power, we need to square it.
  • To verify the scaling law, it may be easier to plot in the log scale.