The baseband equivalent model

Most wireless communication systems send signals at the gigahertz (GHz) frequency. The GHz-frequency spectrum utilized by a wireless communication system is called the passband. However, at the base stations and mobile devices, most signal processing (e.g., coding/decodiing, modulation/demodulation) is done in the baseband, a spectrum centered around zero frequency. Why we process the signals in the baseband and send them in the passband? There are at least two major advantages of this approach.

Interoperability: This approach allows us to have the same baseband signal processing chips for different mobile carriers (e.g., T-Mobile, Verizon), who have separate spectrums. If we were to do signal processing directly in the passband, we would need different processors for different carriers, and the processors would not work when the carrier changes the spectrum (e.g., upgrading from 4G to 5G).
Complexity: The signal processing must be done at an extremely high speed if we process the high-frequency passband signals directly.

Therefore, we upconvert the baseband signal to the passband before sending it from the transmitter, and downconvert the passband signal to the baseband after receiving it at the receiver.

Conversion between baseband and passband signals

Review of Fourier transform

Recall that for any complex-valued signal $s(t)$, the Fourier transform and the inverse Fourier transform are defined as

\[\begin{align} S(f) &= \int_{-\infty}^\infty s(t) e^{-j 2 \pi f t} dt \\ s(t) &= \int_{-\infty}^\infty S(f) e^{j 2 \pi f t} df \end{align}\]

For our discussion, we need the following properties of the Fourier transform:

For any real-valued signal $s(t)$, we have $S(-f) = S^*(f)$. In other words, its spectrum in the negative frequencies is the conjugate of the spectrum in the positive frequencies.
The Fourier transform of $s(t) e^{j 2 \pi f_c t}$ is $S(f-f_c)$. In other words, phase shift in the time domains leads to frequency shift in the frequency domain.

What do negative frequencies mean? Why we never talk about them?

Please see this discussion in StackExchange for the physical meaning of negative frequencies. In short, the complex sinusoid $e^{-j 2 \pi f t}$ at a negative frequency $-f < 0$ is rotating in the opposite direction of the complex sinusoid at the positive frequency $f > 0$.

Although negative frequencies do have physical meanings, we almost never talk about them. This is because in practice, the signals are real-valued, leading to a spectrum with $S(-f) = S^*(f)$. Therefore, we can calculate the negative frequency component from the positive frequency componenet. Since the positive frequency component is all what we need, we focus on the positive frequency domain only.

How to convert between baseband and passband?

Now consider a real-valued passband signal $s(t)$, occuply the spectrum $\left[ f_c - W/2, f_c + W/2 \right]$ of bandwidth $W$ around a center frequency $f_c$. We illustrate its Fourier transform $S(f)$ below:

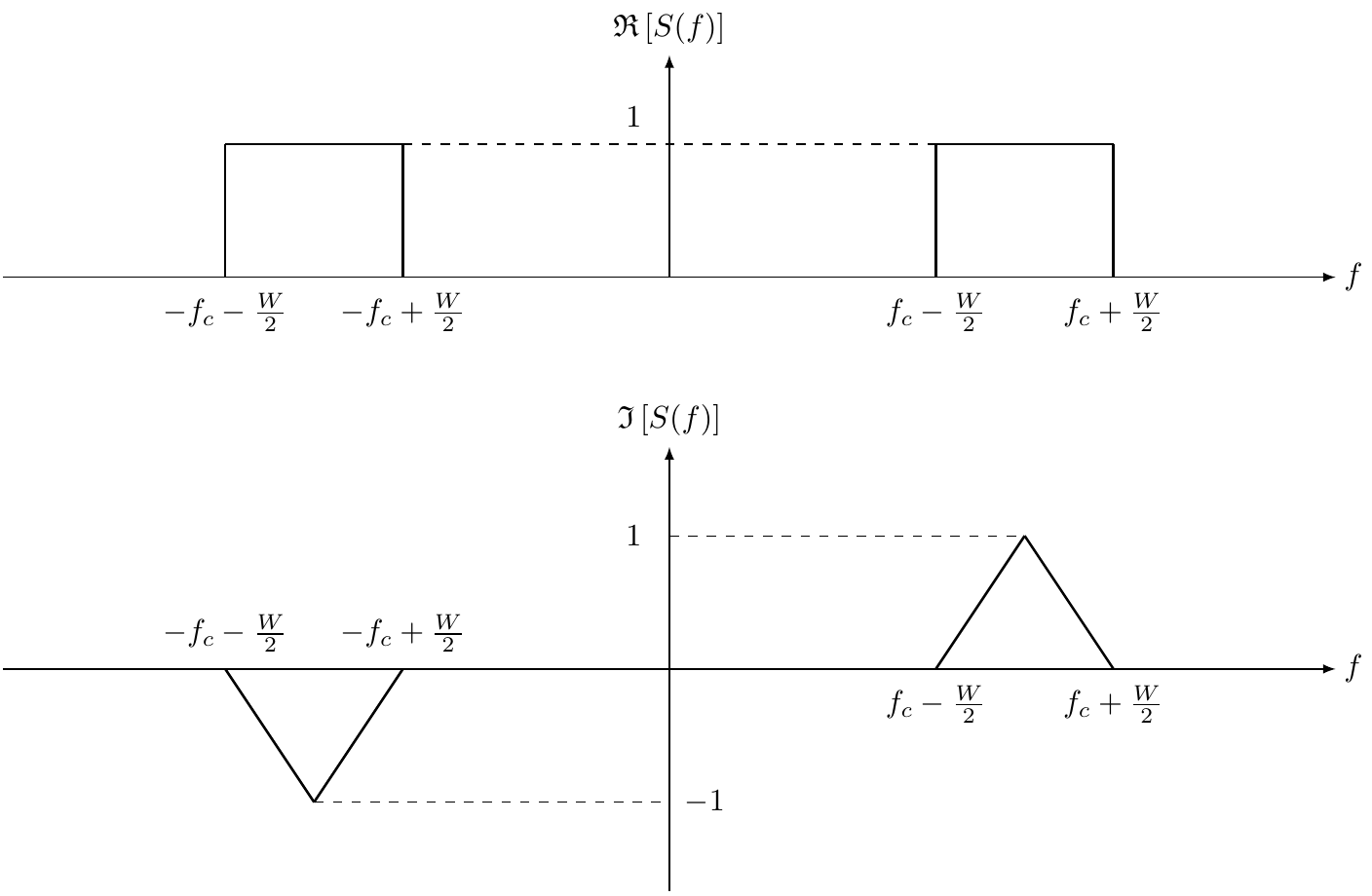
Notice how the real part of the spectrum is symmetric and the imaginary part is antisymmetric, which is a property of Fourier transform of real-valued signals.

The corresponding baseband signal $s_b(t)$ occupies the spectrum $\left[ -W/2, W/2 \right]$ centered around zero frequency:

From the figure, we can see that the baseband spectrum is obtained by shifting the positive frequency component of the passband spectrum to the left. Note that the magnitude of the baseband spectrum is multiplied by $\sqrt{2}$, so that the baseband signal has the same total energy as the passband signal. Therefore, the passband spectrum $S(f)$ can be written in terms of the baseband spectrum $S_b(f)$ as follows \[ S(f) = \frac{1}{\sqrt{2}} \left[ S_b(f-f_c) + S_b^*(-f-f_c) \right]. \]

Using the properties of the Fourier transform, we can obtain the following relationship between the passband signal and the baseband signal

\[\begin{align} s(t) &= \frac{1}{\sqrt{2}} \left[ s_b(t) e^{j 2 \pi f_c t} + s_b^*(t) e^{-j 2 \pi f_c t} \right] \notag\\ &= \sqrt{2} \mathfrak{R}\left[s_b(t)\right] \cos 2 \pi f_c t - \sqrt{2} \mathfrak{I}\left[s_b(t)\right] \sin 2 \pi f_c t \label{eqn:upconversion} \end{align}\]

Equation \eqref{eqn:upconversion} tells us how to upconvert or modulate the baseband signal to the passband. In particular, we can have two streams of signals, which are regarded as the real part $\mathfrak{R}\left[s_b(t)\right]$ and the imaginary part $\mathfrak{I}\left[s_b(t)\right]$ of a complex baseband signal $s_b(t)$. Then we multiply the real part by $\sqrt{2} \cos{2 \pi f_c t}$ and the imaginary part by $-\sqrt{2} \sin{2 \pi f_c t}$, and sum up the products.

To downconvert the passband signal to the baseband, we can multiply the passband signal $s(t)$ by $e^{-j 2 \pi f_c t}$ and pass it through a low pass filter.

Equivalent baseband channel model

Now that we know how to convert between the passband signal and the baseband signal, we can derive an equivalent input/output model of the channel in the baseband.

To derive it, we first note that the relationship between the passband signal and the baseband signal in \eqref{eqn:upconversion} can be rewritten as $\begin{align} s(t) = \sqrt{2} \mathfrak{R}\left[ s_b(t) e^{j 2 \pi f_c t} \right], \label{eqn:passband-baseband-conversion} \end{align}$ which holds true for any signal, including the transmitted signal $x(t)$ or its delayed version $x(t-\tau)$.

Starting from the input/ouput model derived previously, we have

\[\begin{align} y(t) & = \sum_i a_i(t) x(t - \tau_i(t)) \notag\\ & = \sum_i a_i(t) \left\{ \sqrt{2} \mathfrak{R}\left[ x_b(t - \tau_i(t)) e^{j 2 \pi f_c (t - \tau_i(t))} \right] \right\} \notag\\ & = \sqrt{2} \mathfrak{R}\left[ \sum_i a_i(t) x_b(t - \tau_i(t)) e^{j 2 \pi f_c (t - \tau_i(t))} \right] \notag\\ & = \sqrt{2} \mathfrak{R}\left[ \sum_i a_i(t) e^{-j 2 \pi f_c \tau_i(t)} x_b(t - \tau_i(t)) e^{j 2 \pi f_c t} \right] \notag\\ & = \sqrt{2} \mathfrak{R}\left[ \left( {\color{red} \sum_i \left( a_i(t) e^{-j 2 \pi f_c \tau_i(t)} \right) x_b(t - \tau_i(t)) } \right) e^{j 2 \pi f_c t} \right] \label{eqn:passband-receive-signal-1} \end{align}\]

Applying \eqref{eqn:passband-baseband-conversion} to the receive signal $y(t)$, we have

\begin{align} y(t) = \sqrt{2} \mathfrak{R}\left[ {\color{red} y_b(t)} e^{j 2 \pi f_c t} \right] \label{eqn:passband-receive-signal-2} \end{align}

Now comparing \eqref{eqn:passband-receive-signal-1} and \eqref{eqn:passband-receive-signal-2}, we can see that the red parts should be the same, which gives us the input/output model of the baseband channel

\[y_b(t) = \sum_i \left( a_i(t) e^{-j 2 \pi f_c \tau_i(t)} \right) x_b(t - \tau_i(t)).\]

Similar to the case in the passband, we can define the baseband equivalent channel model as \[ h_b(\tau,t) = \sum_{i} a_i^b(t) \delta(\tau - \tau_i(t)), \] where the tap gain is $a_i^b(t) = a_i(t) e^{-j 2 \pi f_c \tau_i(t)}.$

In other words, the baseband equivalent chanenl model is also a FIR filter, but with complex-valued tap gains! The tap gains are complex-valued because the baseband signals are complex-valued.