Case 2: Moving antennas in the free space

Analytical expression

Consider the same two antennas in a free space. But now the receiver is moving away at the speed \(v\) in the direct opposite direction.

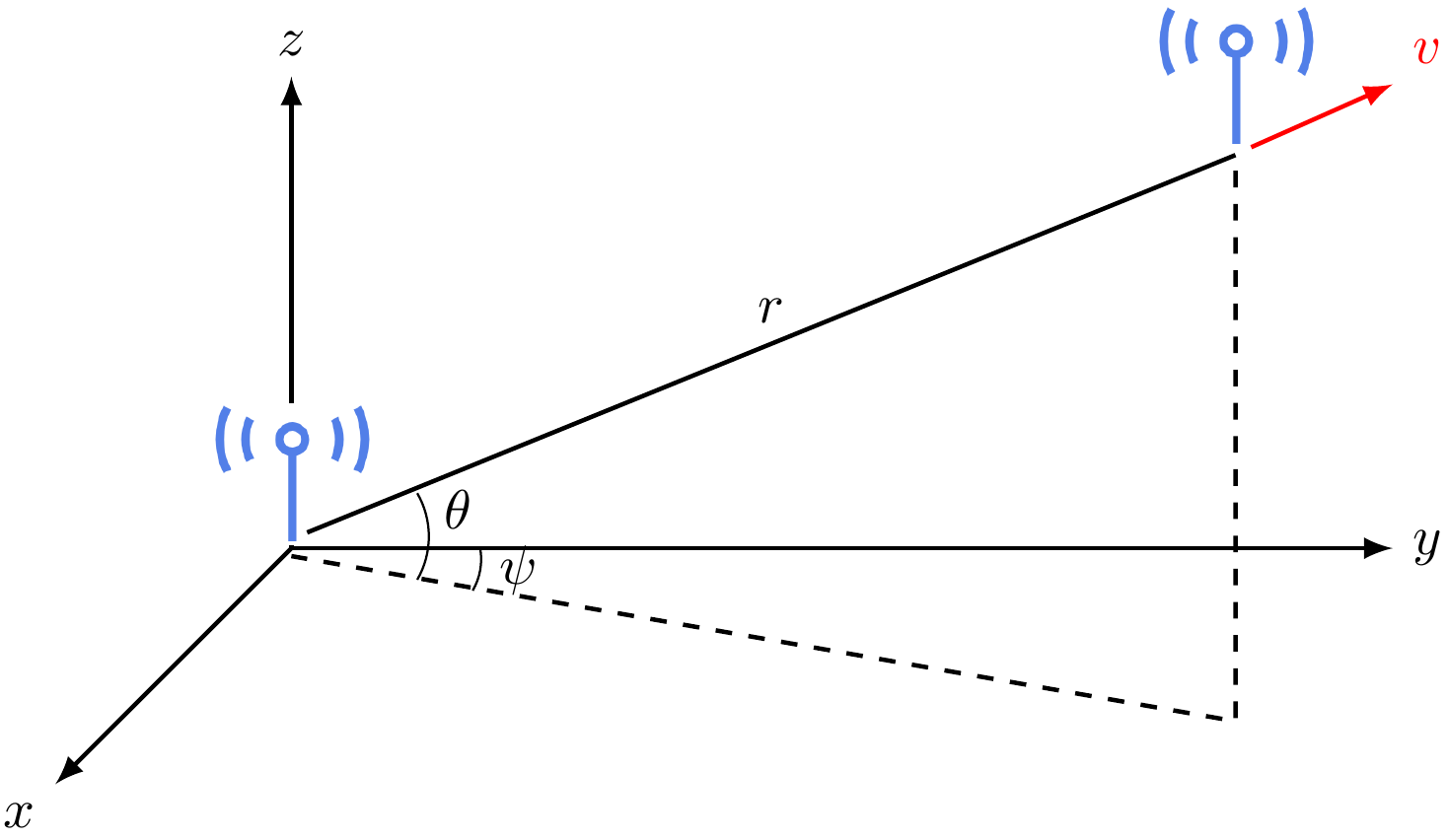
In this case, the location of the receiver antenna is time-varying, namely \[ \mathbf{u}(t) = \left( r(t), \theta, \psi \right), ~\text{with}~ r(t) = r_0 + vt, \] where \(r_0\) is the initial distance at time \(t=0\).

Compared to the case of fixed antennas, the only change is the distance \(r(t)\). Therefore, the received signal is \[ E_r(f,t,(r(t), \theta, \psi)) = \frac{\alpha(\theta,\psi,f) \cos 2 \pi f \left[t - (r_0 + vt)/c\right]}{r_0 + vt} = \frac{\alpha(\theta,\psi,f) \cos 2 \pi f \left[(1-v/c)t - r_0/c\right]}{r_0 + vt}. \]

Doppler shift

The key observation is that the frequency of the received signal changes! In particular, the frequency changes by \(- (v/c) \cdot f\), which is proportional to the moving speed \(v\).

• We may have experienced this in daily life. A siren has a higher frequency (i.e., a higher pitch) when the ambulance is moving towards us, and a lower frequency (i.e., a lower pitch) when the ambulance is moving away.

This phenomenon, where the signal frequency changes when the transmitter and/or the receiver is moving, is called Doppler shift.

In wireless communication systems, we need to take into account the Doppler shift when the moving speed is high. For example, in a high-speed train, it is more challenging to maintain a high-speed wireless connection, partly due to the Doppler shift.